[과천중앙고] 1학년 2학기 기말고사 고난도 문항 손풀이
게시글 주소: https://i.orbi.kr/00065860174
안녕하세요. 어수강 박사입니다.
오늘은 "[과천중앙고] 2023년 1학년 2학기 기말고사 고난도 문항 손풀이를 포스팅" 하도록 하겠습니다.
먼저 17번 문항입니다.


박스의 두 번째 조건을 기준으로 경우 나누기를 하면 되겠죠? 이후 박스의 첫 번째 조건과 세 번째 조건을 만족하는지 확인하면 될 것 같네요. 구체적인 풀이는 다음과 같습니다!
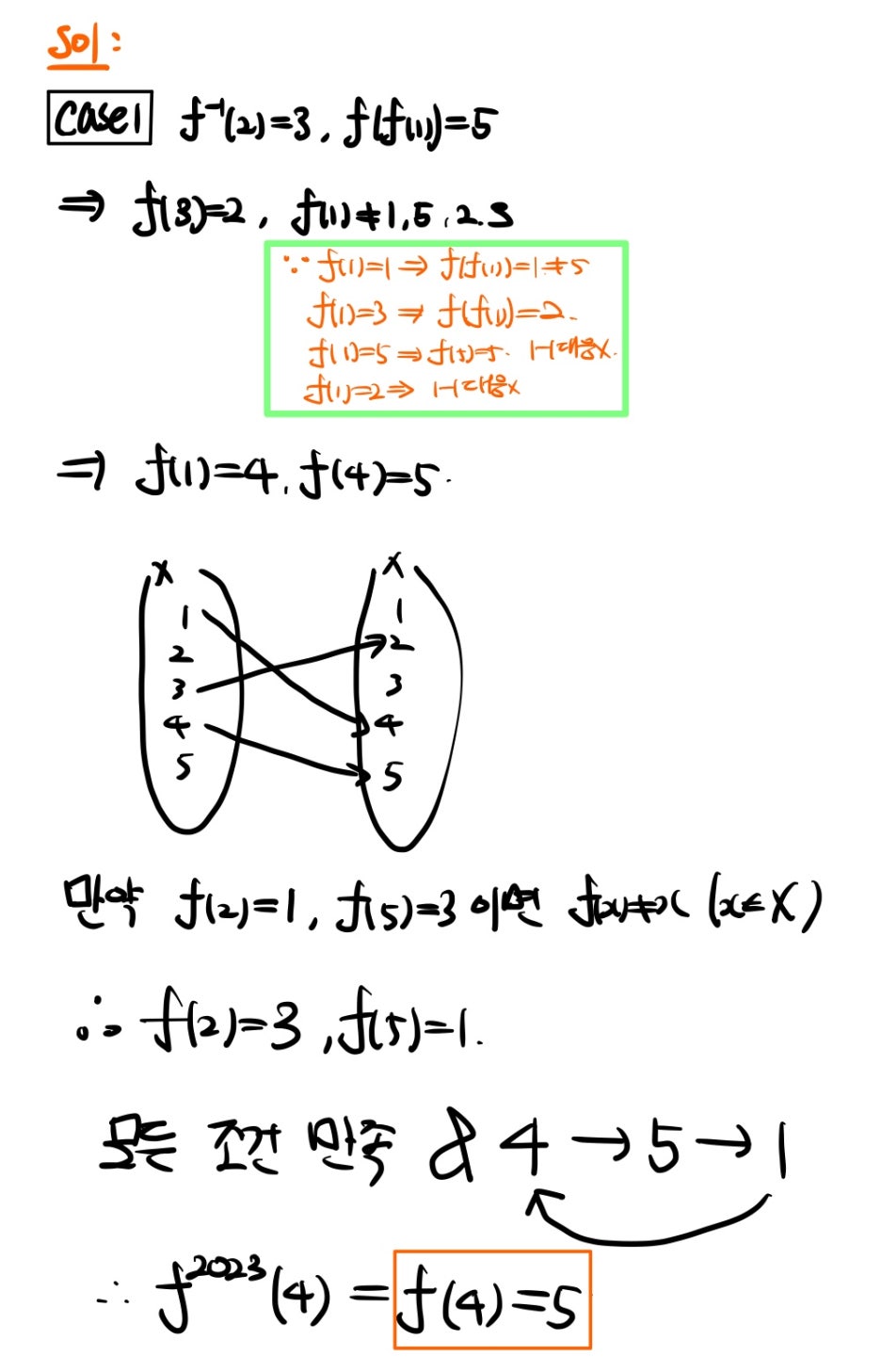

별로 어렵지 않죠? 답은 나왔지만~ Case2도 마저 생각해 볼게요!
(시험에서 case1, case2의 순서가 뒤바뀔 수도 있으니까요 ㅎㅎ)


.
다음은 18번 문항입니다.


대수적으로 풀기 어렵다면 기하적으로 풀면 되겠죠? 함수 y=f(x)의 개형을 그리는 것으로 시작하면 될 것 같습니다.
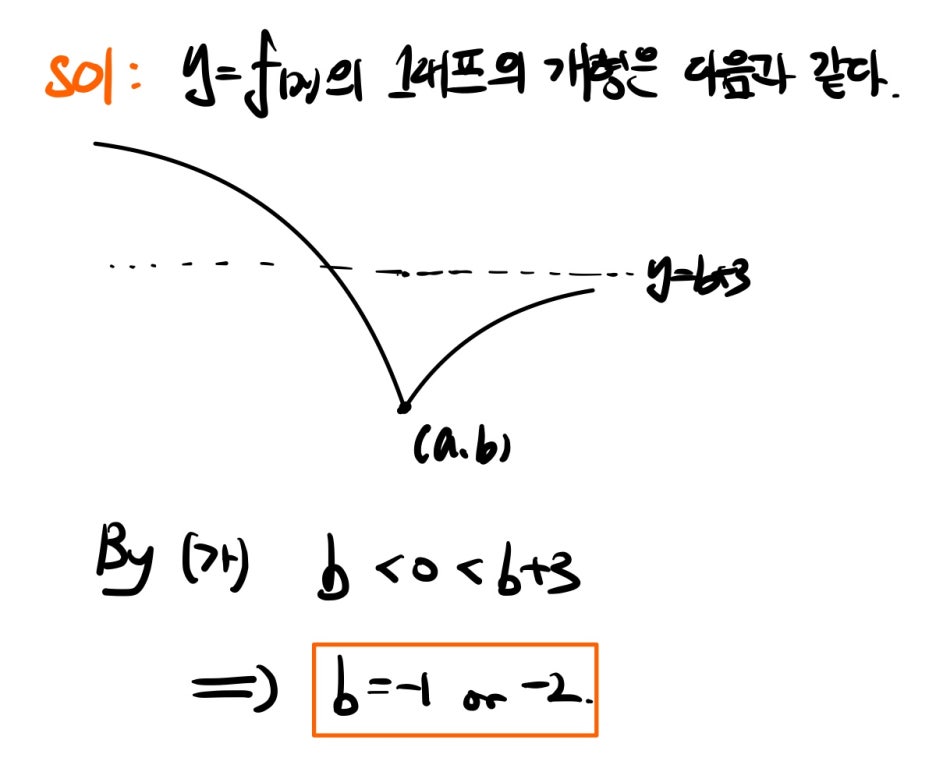

이제 b의 값에 따라 경우를 나누어 풀면 되겠네요! ㅎㅎ 먼저 b=-1인 경우는 다음과 같습니다.
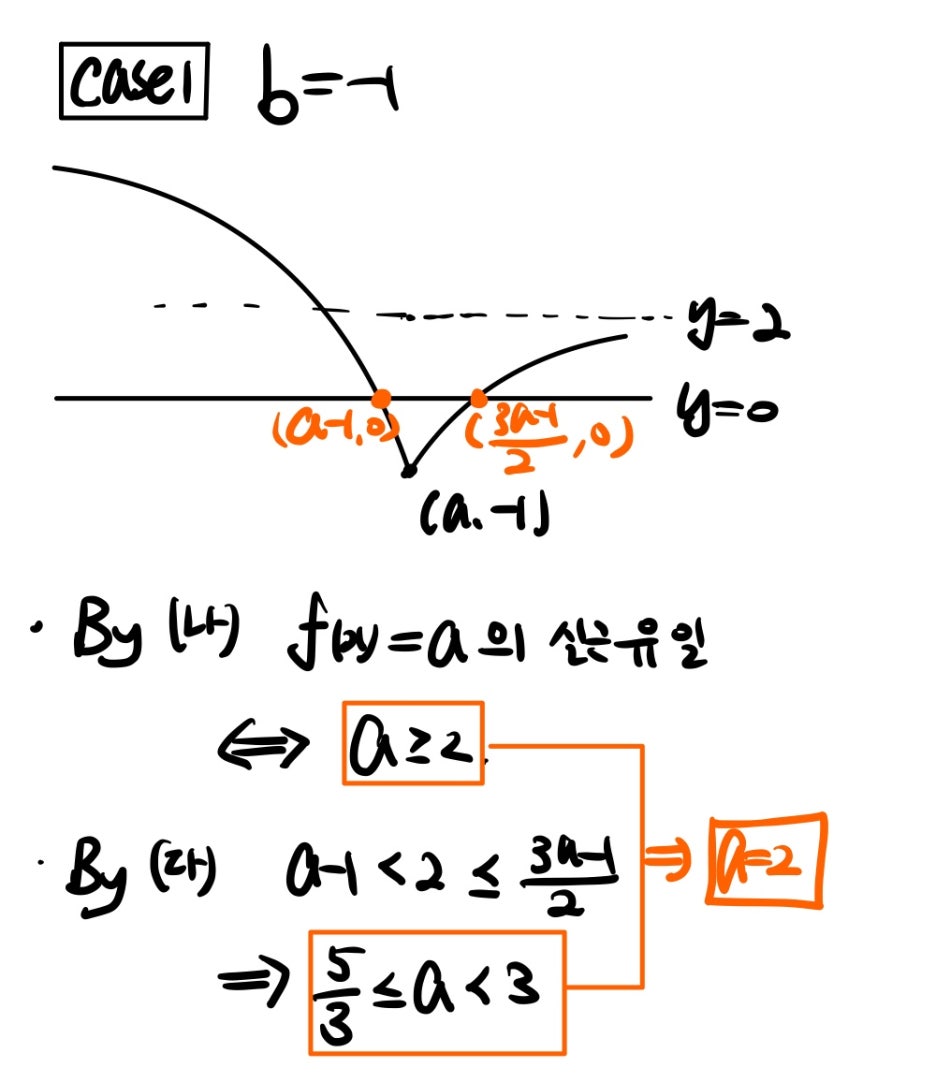

이제 b=-2인 경우만 생각하면 되겠죠?


따라서 답은 다음과 같습니다.

마지막으로 논술형 4번입니다.


복잡해 보이지만 차근차근 풀면 별 거 아니니 쫄지 마세요!ㅎㅎ
저는 조건 (가), (라), (나) 순으로 풀었지만, 순서는 별로 중요하지 않습니다. 하나하나 차근차근 풀기만 하면 됩니다!
저의 풀이는 다음과 같습니다. (참고로 조건 (다)는 쓸모가 없습니다. 왜 저런 조건을 줬을까요?^^;;)
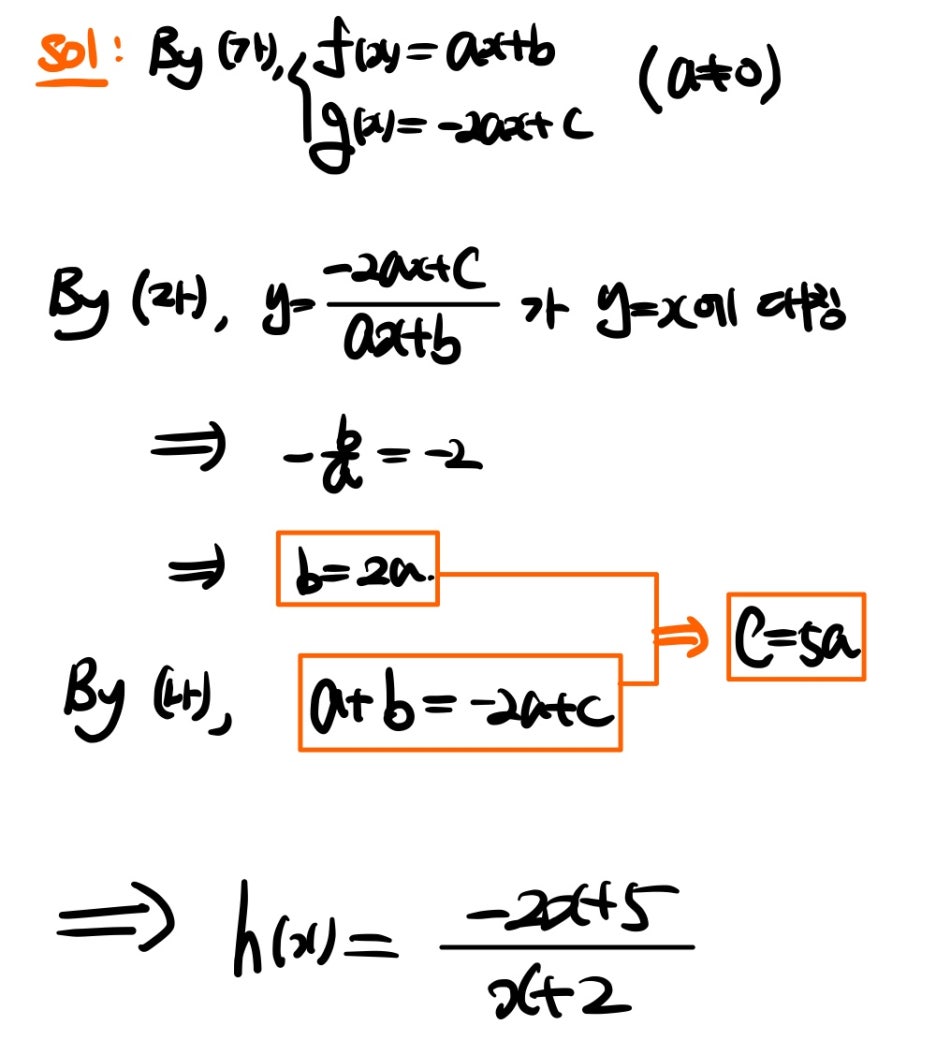

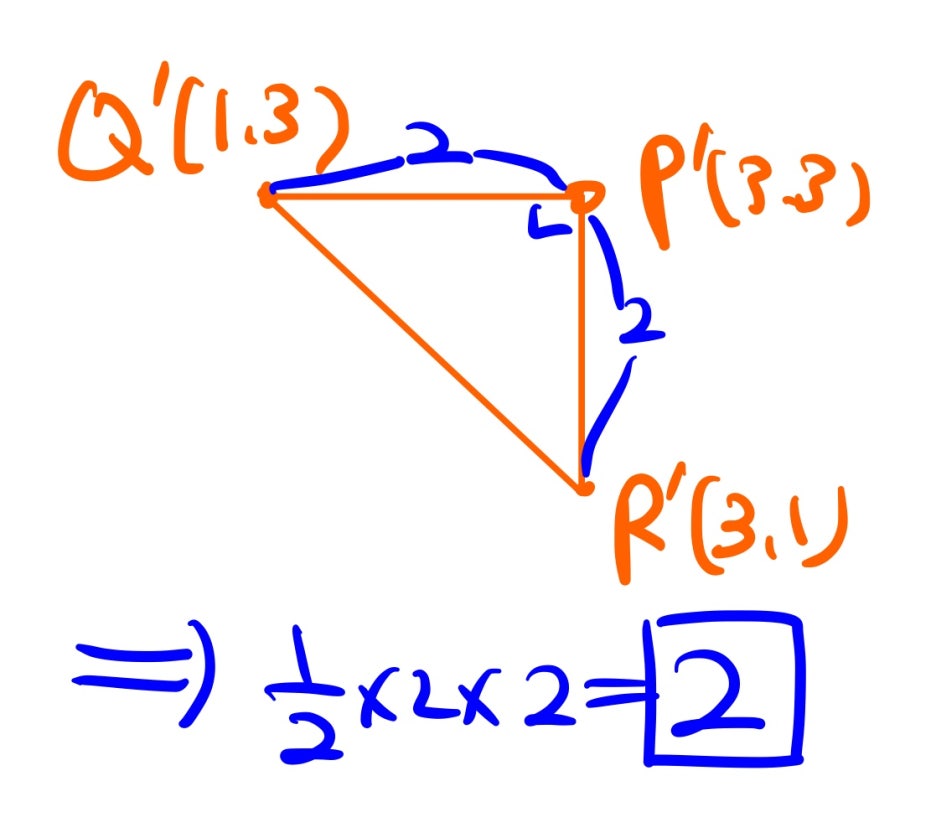
이제 삼각형의 넓이가 최소인 경우를 생각하면 되는데, 계산의 편의를 위해 저는 다음과 같이 평행이동을 했습니다.
평행이동을 해도 삼각형의 넓이는 변하지 않으니 PQR=P'Q'R'이겠죠?


그런데 P'Q'R'의 넓이가 최소가 되는 것은 점 P'에서 선분 Q'R'에 내린 수선의 길이가 최소일 때 입니다. 왜냐하면 이것이 직각이등변삼각형이기 때문입니다!ㅎㅎ


a=3일 때, 삼각형 P'Q'R'의 넓이가 최소이므로~ 이때 넓이를 구하면 되겠죠? 따라서 답은 다음과 같습니다.

기계적으로 문제와 그 풀이를 암기하는 방식으로 공부한 학생이라면 위 세 문항에서 크게 당황 했을 수도 있을 것 같습니다. 하지만 위의 풀이처럼 차근차근 풀면 "[과천중앙고] 2023년 1학년 2학기 기말고사"도 별로 어렵지 않죠?
기계적으로 문제 풀이를 하는 학생을 우수한 학생이라고 생각하는 대학은 없습니다. 배운 것에 근거해서 논리적으로 문제를 해결함으로써 실력을 쌓아나감으로써 우수한 학생이 된다면, 최상위권 대학에서도 여러분을 선발하고자 노력할 거에요. 그러니 그냥 열심히'만' 공부하지 말고, 실력이 쌓이는 방법으로 노력하길 바랍니다!
다음은 실력이 쌓이는 공부 방법에 대한 포스팅 및 전자책 링크입니다.
1. 고난도 문항 치트키 1
2. 고난도 문항 치트키 2
4. 서울대 박사가 알려주는 수학의 비밀 - 첫 번째 비밀 : 집합
5. 서울대 박사가 알려주는 수학의 비밀 - 두 번째 비밀 : 명제
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
뉴진스 0
메리크리스마스
-
ㄹㅇ
-
기분 좋아졌다 2
안경점 사장님이 내가 얼굴이 컸으면 안경테 작기 쉬운데 작아서 딱 맞는 걸...
-
수시 1
두개 붙어서 두개 등록한다음에 1시간 후에 나머지 대학 취소했는데 이중등록임?
-
진학사도 허위표본 있나
-
유리하게 적용될 케이스인가요 불리할까요..???
-
안녕하세요, 저는 2024년에 무휴학 반수를 하고 약대에 입학한 N수생입니다....
-
조건 오댕 프사 or 제가 보기에 성의 있는 댓글(엿장수 맘대로)
-
근데 공군 한능검 가산점 폐지되면 그만큼 컷이 내려감? 5
아니면 헌급방 안하면 못가는데..
-
왜클릭
-
실시간 이원준 4
그러함
-
학원마다 책상 옆에 책 넣어둘수있는 공간 있잖아요 서랍? 그런곳 근데 자꾸 거기...
-
씻으러
-
오늘 업뎃 안하나요…..?
-
예엠병들 한다 시팔
-
저랑 동생한테 투자를 하시느라고 꽤 옛날에 구매하신 옷들을 아직도 입고...
-
나가는 중 0
사람왤케많아
-
받을 수 있는곳이 있나 하,..
-
4 10 7 1 순서로 빠졌는데 6번짼데 가능성 있으려나 남은거 이거 하나라 안되면...
-
ㄹㅇ임? 어디서 하는데? 나 연락할 애가 없어서 너무 심심하다 ㅜ
-
지사의 질문있는데 12
고조완관건제중 하나인데 여기 의대는 마이너과 못가나요?
-
나 생일임 19
-
의사=공공재 ㄷㄷㄷㄷㄷ
-
ㅇㅇ
-
알겠어 기하하면되잖아. 확통사탐 안한다고.
-
개인적으로 좋아해요
-
둘다 가격은 같음
-
국어 수학 과외 5
보통 커리가 어케 되나요 책은 쌤이 정하는 건가요
-
수학 좋아합니다.어디가 낫나요
-
아 재밌어 5
방학이 이래서 좋지. 애니 정주행 캬
-
강남갈까 대치갈까
-
의평원 자켜보고 전적대로 돌아갈려하는데 근데 하..약대로 돌아가기 너무 싫은데 그냥 지금 자퇴할까
-
현우진 시발점 12
시발점 할때 시발점 워크북하고 쎈이나 rpm같은 유형서 필수인가요? 아니면 워크북만...
-
원회에 의해 제삭된 물시게입니다
-
크리스마스 이브 감성도 무뎌질까?
-
경희대학교 유전생명공학과 25학번 단톡방 안내 안녕하세요 유전생명공학과...
-
이거 무조건 되나여??
-
오늘 폭식함 2
아이스크림 돈가스 콜라까지
-
3합 5.5면 장학 아예 없나요 ... 하
-
진학사 2
6시에 업뎃한다면서 30분 미뤘네 짜증나게....
-
알바끝 3
이제 엄마만나러감 히히 클스마스에는 가족과 :)
-
게시물에 의해 회원된 삭제입니다.
-
원과목 다시 살아남?
-
저녁여캐투척 8
대황덴
-
그런 느낌이네요
-
뭔가 심하게 괴리가 있는거 같아서요….지금부터 갑자기 몇배가 들어와야 저 칸수가 맞는데
-
고려대 변표 5
나온거임?
-
추천 부탁드려요 어법 1시간 독해 1시간 예정이에요






















































아, 참고로 14번 문항은 오류입니다. (k=-5이면 상수함수가 돼서 ㄱ, ㄴ, ㄷ가 모두 거짓이 됩니다^^;;) 집합에서 구별법을 공부해야 한다고 강조했는데~ 분수함수인지 아닌지 구별하는데 신경을 안 쓴 것이 오류의 원인이 된 듯 합니다.