"Chapter. 0 - 함수의 연속"
게시글 주소: https://i.orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

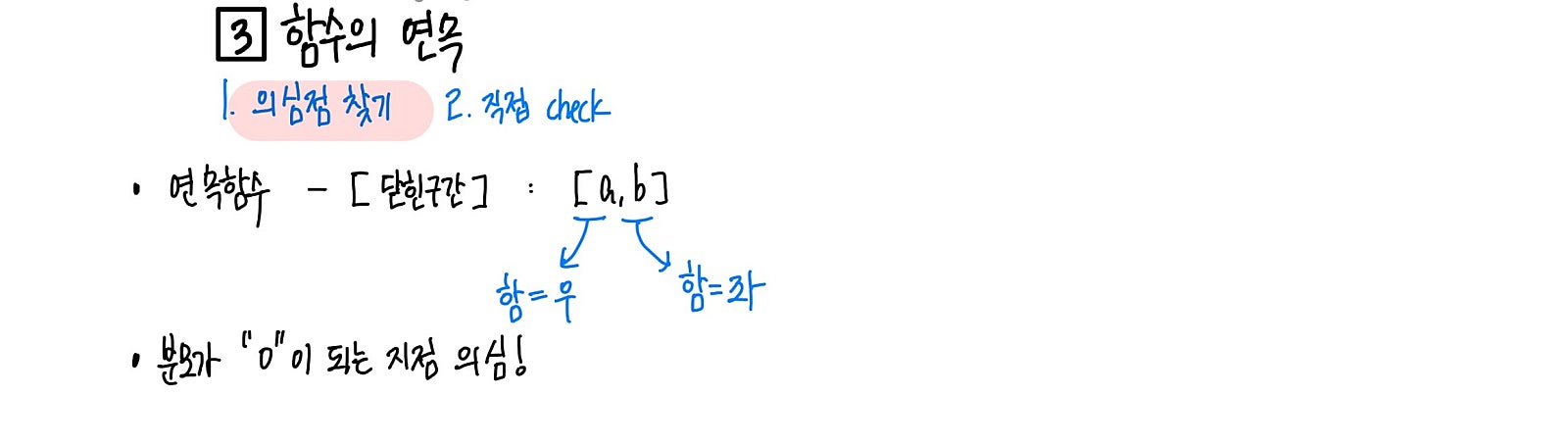
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
양쪽 다 있네 ㅎㄷㄷ
-
정시인가요? 벌써 발표를 ㄷㄷ?
-
가즈아
-
나도이제약대생? 11
일케 올리면 되나
-
Orbi지형T_[점수를높이는5M.Column] Ch1.등차수열'지형도를그리다' 6
[5-Minute Column] "Major Past Math Questions...
-
뱃지 나왔어요 17
똥테랑 잘어울리네요 ^^
-
ㅈㄴ부럽네 진짜
-
잘잣다 4
-
업보청산
-
는 언제나 당연한 거고 이거 좀 보세요 https://orbi.kr/00071308476
-
내신 고2 수학 8
예비 고2 준비하는 학생입니다.개념 잡고 모의고사 문제를 풀면 고2모 기준...
-
현재 고2이고 고1 수학에 빵꾸가 많이 나서 메꾸고 수1을 들어야 할 것 같습니다....
-
계속 귀여운척하면 진짜 귀여어 질지도 몰라요!!!
-
39명 모집에 240명 지원했어요 ㅈ바류ㅠ
-
탄핵찬성하는 얘들이 14
윤석열 체포하는거 보면서 좋아하는거 보면 아이러니함
-
약대 ㅇㅈ 17
우오오오오옹
-
속아주는 척이라도 해주세요
-
앞으로 자작 국어 관련 내용 아니면 글 안 쓸 거임.. +) 제가 이상한 소리 하는...
-
파카= 잉크회사 0
파카는 좋은 잉크회사이다. 착한 파카는 죽은 파카뿐이다.
-
기를 썼네
-
덕코 내놧 8
내놧
-
정치커뮤를 하면 11
정치공부 직빵이에요 동시에 본인의 희망 학과가 사회과학대학 안에 있게 되는 경험을...
-
늘 느끼던건데 이름 귀여움 재료
-
첨언 부가함 1
참고로 메이저 지거국도 기준마다 ㅈㄴ 다름 애초에 부산대나 경북대같은 메이저 지거국...
-
극보수 극좌파 유튜버를 동시에 구독해서 영상을 주기젇으로 같이 보면 공부됨 +나무위키 —> 정잘알됨
-
모의면접 이거는 안해도되는거 맞나요?? 실제면접만 응시하면 되는거죠? 모집요강...
-
평가원 #~#
-
ㄱㄱ
-
하나도 모름..
-
尹대통령, 관저 나서며 "국민들과 함께 끝까지 싸울 것" 13
[파이낸셜뉴스] 윤석열 대통령이 15일 한남동 관저에서 이동하기 전 "국민들과 함께...
-
정치 공부는 뭘로 해야함..? 국회의원도 잘 모르고 암튼 여러모로 잘 모르는데
-
정치성향 중요하게 보려나
-
둘 중 어디 선택하나요? 이런 경우 지거국 선택하는게 좋지 않요까요? 수만휘에...
-
자전거사고싶다 4
ㅠㅠㅠㅜ
-
스크류형 만듦샤 개 ㅅㅂ이네 또 고장남 뻐커 이 ㅅㅂ것들
-
미분이 진짜 꼴리는데 36
나의 천박한 손놀림으로 함수를 미분하는거지... 한꺼풀 한꺼풀씩 벗기다보면 그녀의...
-
중대 1시 조발 1
안 하나
-
빅펌들어할때
-
아니면 일반전형으로 생기는거임?
-
옯스타이지만 이제 공부얘기만 올라오는 올브타에 대해서… 매일매일 수능전까지 하루도...
-
님들아 어제 올린 글이 단순 자랑글이 절대 아니라는 거 4
특히 공대 지망하는 수험생분들이나 공대 신입생들 위해서 미리 붙여두는 정보임 공대는...
-
한동훈은 2
그냥 민주당으로가라..
-
쪽지 주세요
-
캬 드디어 정신차렸구나
-
그녀가 숙소 잡았다는데 11
잘 될까요 낼 생일이라 부산 1박 2일 놀러감…0
-
mbc보고 1
채널에이도 보는게 좋은듯
-
엄청 세세한 분석은 오버
-
엄마<——최고의 요리사 그냥 goat.
-
설사범 면접 2
잘 보면 가산점 얼마만큼 주나요? 성적은 안정권인데 궁금해서요



















































